Part1 高温加速模型:阿伦尼斯Arrhenius【适用场景】阿伦尼斯模型适用于单纯考虑热效应试验的加速模型,当温度是影响产品老化及使用寿命的绝对因素时,采用该加
Part1 高温加速模型:阿伦尼斯Arrhenius
【适用场景】
阿伦尼斯模型适用于单纯考虑热效应试验的加速模型,当温度是影响产品老化及使用寿命的绝对因素时,采用该加速模型来模拟整个寿命周期的可靠性表现。
【加速因子公式表达】
加速因子公式表达:
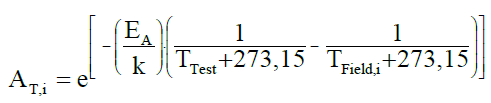
其中公式中各个参数代表的含义解释如下
AT,i:加速因子,在所有的加速模型中都是表达一个含义,也就相当于加速系数,计算出他就能将整个寿命周期时间转换成加速试验的时间;
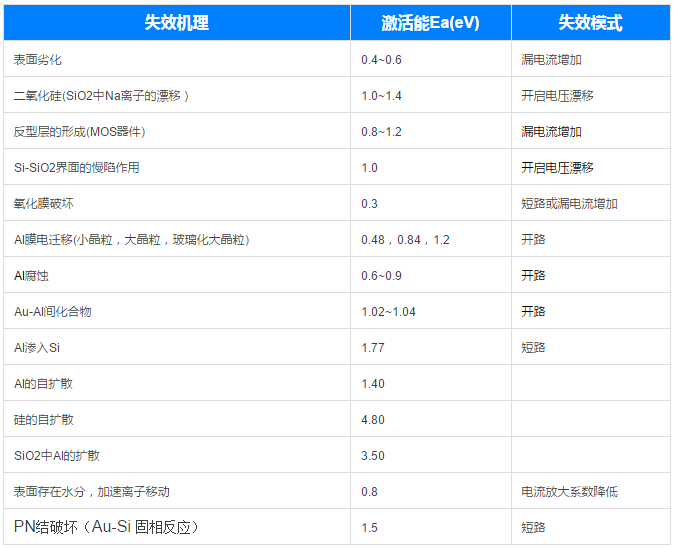
Ea:是析出故障的耗费能量,又称激活能。不同产品的激活能是不一样的。一般来说,激活能的值在0.3ev~1.2ev之间;
K:是玻尔兹曼常数,其值为8.617385×10-5 ev/K;
Ttest:测试条件下(加速状态下)的温度值。此处的温度值是绝对温度值,以K(开尔文)作单位;
Tfield:是使用条件下(非加速状态下)的温度值。此处的温度值是绝对温度值,以K(开尔文)作单位
【理论背景引入】
玻尔兹曼常数:(玻尔兹曼是一位奥地利物理学家)

开尔文定义为“对应玻尔兹曼常数为1.380649×10-23J/K的热力学温度;玻尔兹曼常量系热力学的一个基本常量。
温度完全由气体分子运动的平均平动动能决定 [3] 。也就是说,宏观测量的温度完全和微观的分子运动的平均平动动能相对应,或者说,大量分子的平均平动动能的统计表现就是温度(如果只考虑分子的平动的话)
阿伦纽斯:瑞典化学家

从公式中可以看出,激活能越大,加速系数也越大,越容易被加速失效,加速试验效果越明显;
在激活能确定的情况下,温度差越大,加速系数也越大;
还有个知识点:活化能的概念和推导;大家可以自己查找相关资料了解一下这个参数的实践得出的过程。下面示例帮忙阐述活化能失效的概念:
【实操计算】:
案例:某一客户需要对产品做105℃的高温测试。据以往的测试经验,此种产品的激活能Ea取0.68最佳。对产品的使用寿命要求是10年,现可供测试的样品有5个。若同时对5个样品进行测试,需测试多长时间才能满足客户要求?
解:AF=EXP(Ea/k*(1/Tnormal-1/Tfeild))=exp(0.68/K*(1/((25+273)-1/(105+273)))=262
T测=Life/AF=10*365*24/262=333.73h
Part2 阿伦尼斯Arrhenius 应用于高温间隙的试验循环
【适用场景】
基于上一页介绍的Arrhenius基础模型介绍,当产品在某一个温度时会出现性能降低(一般设计规范里会给出),而温度分布的区间又大于该温度,为了模拟产品真实的应用环境,就需要间歇在测试温度Topmax和Tmax时进行测试;
【公式表达】
基本公式不变,变化的是:
1、对于测试温度需要根据温度分布的谱范围做调整,低于Topmax的测试温度取Topmax,高于Topmax的测试温度取Tmax;
2、分布计算每一个温度点对应的AF加速因子值;然后按照分布的比重计算加速后需要的时间,加速总时间即为这些时间的累加;
【实操计算】
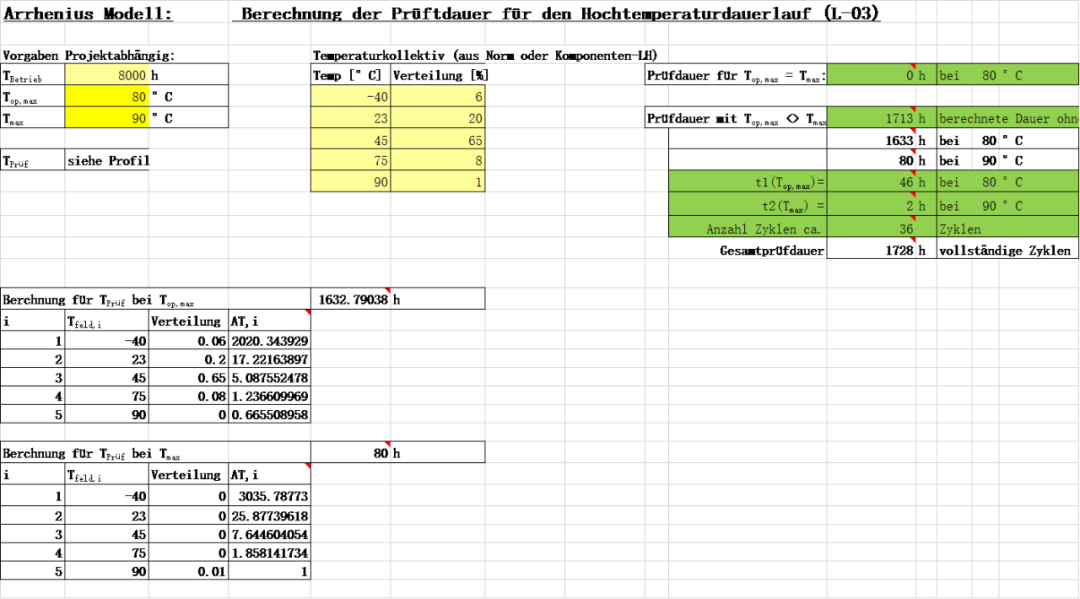
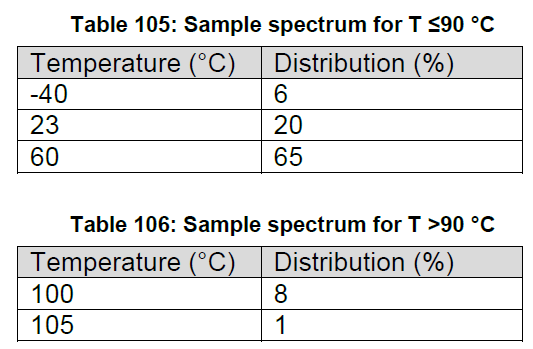
比如说,VW80000中某款产品的使用使命8000h,90°时产品性能开始降低,分布分布的谱范围如下,试计算间歇加速时间分布和加速后试验时间?
计算表格公式如下: